题目地址

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：
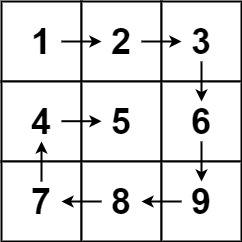
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：
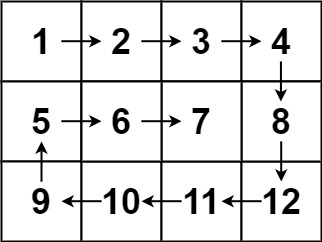
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

解法

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        //判断边界
    vector <int> ans;
    if (matrix.empty()) return ans;
      //首先找到四个角落
    int row = matrix[0].size();
    int column = matrix.size();
    int left = 0;
    int top = 0;
    int right = row - 1;
    int under = column - 1;
    while (left <= right && top <= under) {
        //输出顶部
        for (int i = left; i <= right; i++) {
            ans.push_back(matrix[top][i]);
        }
        //输出右边
        for (int i = top + 1; i <= under; i++) {
            ans.push_back(matrix[i][right]);
        }
        //判断是否到了底部
        if (left < right&& top < under) {
            //输出下
            for (int i = right - 1; i > left; i--) {
                ans.push_back(matrix[under][i]);
            }
            //输出左
            for (int i = under; i > top; i--) {
                ans.push_back(matrix[i][left]);
            }
        }
        //缩圈
        left++;
        right--;
        top++;
        under--;
    }
    return ans;
  }
    };

//按照层次模拟
    class Solution {
        public List<Integer> spiralOrder(int[][] matrix) {
            //边界判断
            if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
                return new ArrayList();
            }
            //首先找到四个角落
            int row = matrix[0].length;
            int column = matrix.length;
            int left = 0;
            int top = 0;
            int right = row - 1;
            int under = column - 1;
            //循环
            List<Integer> res = new ArrayList(row * column);
            while (left <= right && top <= under) {
                //输出上
                for (int i = left; i <= right; i++) {
                    res.add(matrix[top][i]);
                }
                //输出右
                for (int i = top + 1; i <= under; i++) {
                    res.add(matrix[i][right]);
                }
                //判断是否到了底部
                if (left < right && top < under) {
                    //输出下
                    for (int i = right - 1; i > left; i--) {
                        res.add(matrix[under][i]);
                    }
                    //输出左
                    for (int i = under; i > top; i--) {
                        res.add(matrix[i][left]);
                    }
                }
                left++;
                right--;
                top++;
                under--;
            }
            return res;
        }
    }
}

解题思路

按层模拟

很久没写关于leetcode的题解了，这题属于leetcode虽然属于中等难度的题目，解法还是比较简单的、

1.首先设定上下左右边界
2.其次向右移动到最右，最右边移动到右下角，右下角到左下角，再左下角继续向上输出，就是首先输出最外层的元素，再缩小一圈输出次外层的元素，直到输出最内层的元素

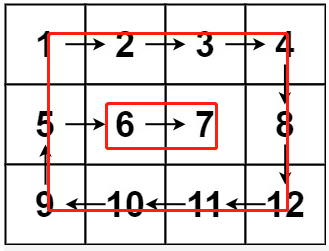
这题最重要的地方是四个角的条件判断
1.从最左边到右边的判断条件

int i = left; i <= right; i++

2.最右边移动到右下角

int i = top + 1; i <= under; i++

当到了右下角时，这里需要注意一点，其中1，12已经输出过了，需要判断不能再次输入(PUSH)

//避免重复的输入

  left < right&& top < under

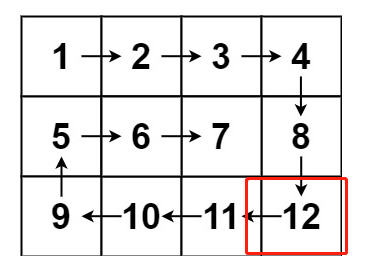
3.右下角到左下角

int i = right - 1; i > left; i--

4.右下角到左下角

int i = under; i > top; i--