974. 和可被 K 整除的子数组
题目描述
给定一个整数数组 A，返回其中元素之和可被 K 整除的（连续、非空）子数组的数目。
示例：
输入：A = [4,5,0,-2,-3,1], K = 5
输出：7
解释：
有 7 个子数组满足其元素之和可被 K = 5 整除：
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
提示：
1 <= A.length <= 30000
-10000 <= A[i] <= 10000
2 <= K <= 10000
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/subarray-sums-divisible-by-k
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
解法
JAVA
class Solution {
public int subarraysDivByK(int[] A, int K) {
Map<Integer, Integer> record = new HashMap<>();
//考虑全部得前缀和会整除K；
record.put(0, 1);
int sum = 0;
int res = 0;
for (int i : A) {
sum+=i;
int module=(sum % K + K) % K;
int same = record.getOrDefault(module,0);
res+= same;
record.put(module,same+1);
}
return res;
}
}
C++
class Solution {
public:
int subarraysDivByK(vector<int>& A, int K) {
unordered_map<int, int> record = {{0, 1}};
int sum = 0, res = 0;
for (int elem: A) {
sum += elem;
int modulus = (sum % K + K) % K;
if (record.count(modulus)) {
res += record[modulus];
}
record[modulus]++;
}
return res;
}
};
解题思路
前缀和
对!今天的题解有两个，因为我开始学习C++了。从今天开始，我会尝试使用两个语言写题解！！
解题之前，我们先了解两个知识点
前缀和
用sum[i]表示S[1]+S[2]+...+S[i]，则sum[0] = 0, sum[1] = S[1], sum[2] = S[1]+S[2]; sum[3]=S[1]+S[2]+S[3];
则S[0]+S[1]+S[2]+...+S[i] = sum[i]==》S[i]=sum[i]-sum[i-1]
sum[i]可以有之前的元素推导出来，如同前缀一般，转换成公式为
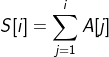
常用于快速处理区间加减操作或者连续子数组问题
同余定理
数论中的重要概念。给定一个正整数m，如果两个整数a和b满足a-b能够被m整除，即(a-b)/m得到一个整数，那么就称整数a与b对模m同余，记作a≡b(mod m)。对模m同余是整数的一个等价关系。
由以上两点可以得出
sum(i, j) =S[j]−S[i−1]，如果sum(i, j)%k=0,满足被 K 整除，推导出 (S[j]−S[i−1])%m=0,即
S[i-1]%k=S[i-1]%k；所以我们只要统计S[i-1]%k=S[i-1]%k的存在的个数，就能直到答案了。
S[i-1]%k作为key存入map中，遇到相同的key则表明存在一个sum(i, j) 可以被K整除，讲map的value++.
同时我们也要考虑前缀和本身被 K 整除的情况。我们直接初始化map，record[0]=1。
我对于int modulus = (sum % K + K) % K;这里不太理解,这里的
可以记为
int temp = sum % K;
if (temp < 0) temp += K;
我们计算-3%5,在java中计算出的结果为-3，我们需要对这个-3进行处理转换为正数，以5为模，我们-3需要讲-3转换为正数表示，我们将使用-3理解为0-3，0+(5-3)，同时将0去掉，则
-3=5-3=2
即负数可以用模减去这个负数的绝对值表示，调换位置 -3=-3+5
这里的转换可以参考下面这个思路
假如现在是6点，想知道3个小时前是几点，我们可以直接把时针逆时针旋转3个小时，也可以顺时针旋转9个小时，得到的时间是一样的。用数学语言我们可以这样表示:
6 - 3 = 6 +（12 - 3）
怎么计算值呢？6-3=6+9=15,15对12取模等于3
这样我们再可以根据同余定理
(-3%5)%5=(-3+5)%5,再用k代替5 (sum % K + K) % K