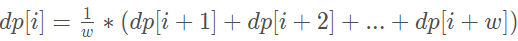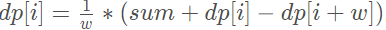题目描述
爱丽丝以 0 分开始，并在她的得分少于 K 分时抽取数字。 抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。 每次抽取都是独立的，其结果具有相同的概率。
当爱丽丝获得不少于 K 分时，她就停止抽取数字。 爱丽丝的分数不超过 N 的概率是多少？
示例 1：
输入：N = 10, K = 1, W = 10
输出：1.00000
说明：爱丽丝得到一张卡，然后停止。
示例 2：
输入：N = 6, K = 1, W = 10
输出：0.60000
说明：爱丽丝得到一张卡，然后停止。
在 W = 10 的 6 种可能下，她的得分不超过 N = 6 分。
示例 3：
输入：N = 21, K = 17, W = 10
输出：0.73278
提示：
0 <= K <= N <= 10000
1 <= W <= 10000
如果答案与正确答案的误差不超过 10^-5，则该答案将被视为正确答案通过。
此问题的判断限制时间已经减少。
解法
JAVA
class Solution {
public double new21Game(int N, int K, int W) {
if (K == 0) {
return 1.0;
}
double[] dp = new double[K + W+1];
double sum=0.0D;
for (int i = K; i <= N && i < K + W; i++) {
dp[i] = 1.0;
sum+=dp[i];
}
for (int i = K - 1; i >= 0; i--) {
dp[i] =sum/W;
sum=sum-dp[i+W]+dp[i];
}
return dp[0];
}
}
解题思路
DP(动态规划）
思路借鉴还有比这更简单的题解吗？填格子游戏开始
首先我们理解一下这道题目的规则
- 抽取时，她从
[1, W]的范围中随机获得一个整数作为分数进行累计
从1到w中随机取到一个数字，根据每个数字被取到的概率为1/W - 爱丽丝以 0 分开始，并在她的得分少于 K 分时抽取数字
如果第一次抽的是1，第二次为2，以此类推，当抽取i次，手上的抽取的牌的综合为 sum=1+2+3+.....+i.，当sum>=K，停止抽取，如果还小于K，继续抽取从1到w中随机取到一个数字 - 爱丽丝的分数不超过 N 的概率是多少？
如果，第i次抽取时，总和sum>=k，停止抽取，如果sum<N，获胜，sum>N，则失败
那如果手上的牌总和X呢？由于再一次从 [1, W],抽取每一个数字的概率都为1/w,由于我有w种可能，如X+1，X+2~X+W,那么当前获取的获胜的概率为，所有的抽取的概率的和除以抽取的次数
dp[X]= (dp[X+1]+dp[X+2]~dp[X+W])/W；
这里的dp[X+1]，表示下一次抽到1的几率。
- 如果X=K，停止抽牌，那么我牌总和最大为K-1，我最大抽取的牌为K-1+W,
- 当抽到了K，并且总和还小于N，那么我后面继续抽取K,K+N之间的胜率为100%，虽然题目要求不能抽取吗，那么K点的胜率是多少呢？
==>dp[K]=(dp[k]+dp[k+1]~dp[N]+0)/W；其中K<N;N<K+W
N以后的胜率为0不进行累计
double sum=0.0D;
//如果N的大于K;最多抽取K+W次，其中K~N的胜率都是1
for (int i = K; i <= N && i < K + W; i++) {
dp[i] = 1.0;
sum+=dp[i];
}
后面的K~N的几率累计，这里由于几率都是1.0就没有除以次数
那么K-1的概率为多少?
由之前的公式可以得出
dp[K-1]= (dp[k-1+1]+dp[k-1++2]~dp[k-1+W])/W；
由于N之后的胜率都是0
==>dp[K-1]=(dp[k]+dp[k+1]~dp[N]+0)/W；
其中我们之前计算dp[K]之后为sum,这里我们使用
=>sum/w；
那么下一个的几率为多少？
sum+=dp[i]-dp[i+W];
这个地方，目前还没理解，本来打算想换个题目写题解，但是觉得这个题目很有趣，就写了点思路，欢迎大家关于这点推导，在评论指导一下
