每日题解:LeetCode 718. 最长重复子数组
2020-07-01
题目描述
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。
提示:
1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100
解法
JAVA
class Solution {
public int findLength(int[] A, int[] B) {
int lenA = A.length;
int lenB = B.length;
int ans = 0;
for (int i = 0; i < lenA; ++i) {
int len = Math.min(lenB, lenA - i);
int maxLen = finMaxLen(A, B, i, 0, len);
ans = Math.max(ans, maxLen);
}
for (int i = 0; i < lenB; ++i) {
int len = Math.min(lenA, lenB - i);
int maxLen = finMaxLen(A, B, 0, i, len);
ans = Math.max(ans, maxLen);
}
return ans;
}
private int finMaxLen(int[] A, int[] B, int addA, int addB, int len) {
int ret = 0, k = 0;
for (int i = 0; i < len; i++) {
if (A[addA + i] == B[addB + i]) {
k++;
} else {
k = 0;
}
ret = Math.max(ret, k);
}
return ret;
}
}
CPP
class Solution {
public:
static int findLength(vector<int> &A, vector<int> &B) {
//DP[i][j]
int ans = 0;
int lenA = A.size();
int lenB = B.size();
vector<vector<int>> dp(lenA + 1, vector<int>(lenB + 1, 0));
for (int i = lenA - 1; i >= 0; i--) {
for (int j = lenB - 1; j >= 0; j--) {
dp[i][j]=A[i]==B[j]?dp[i+1][j+1]+1:0;
ans=max(ans, dp[i][j]);
}
}
return ans;
}
};
解题思路
最简单的写法是三层循环,逐步对比字符是否相等,然后往后遍历,
for(){
for(){
while(){
}
}
}
但是这题的测试用例会出现超时的问题,所以就需要减少循环的次数
滑动窗口
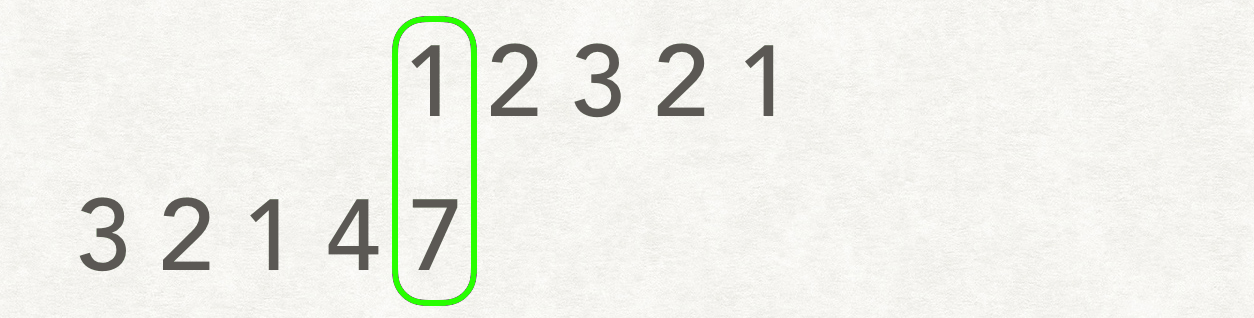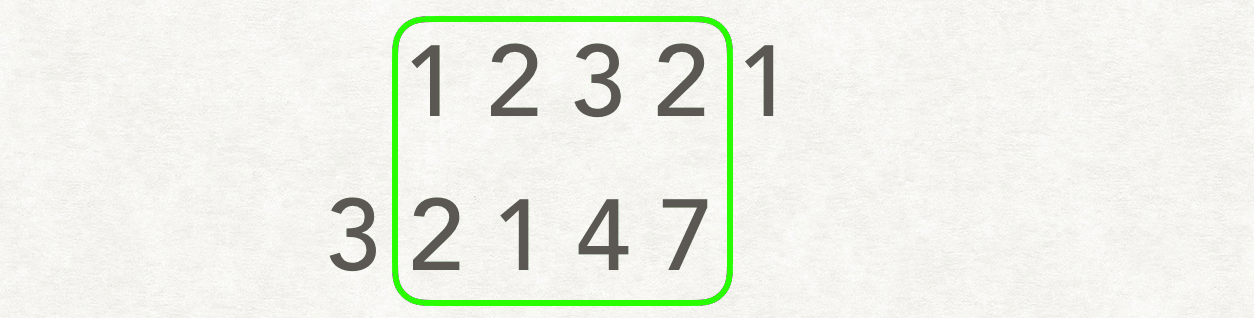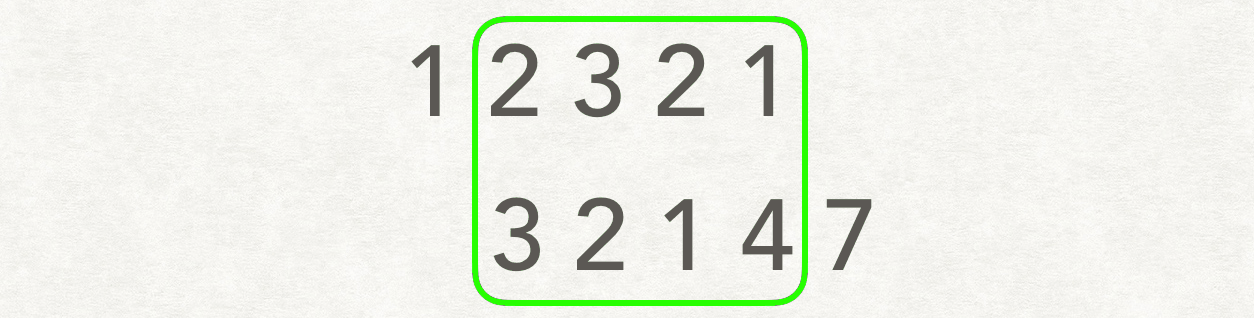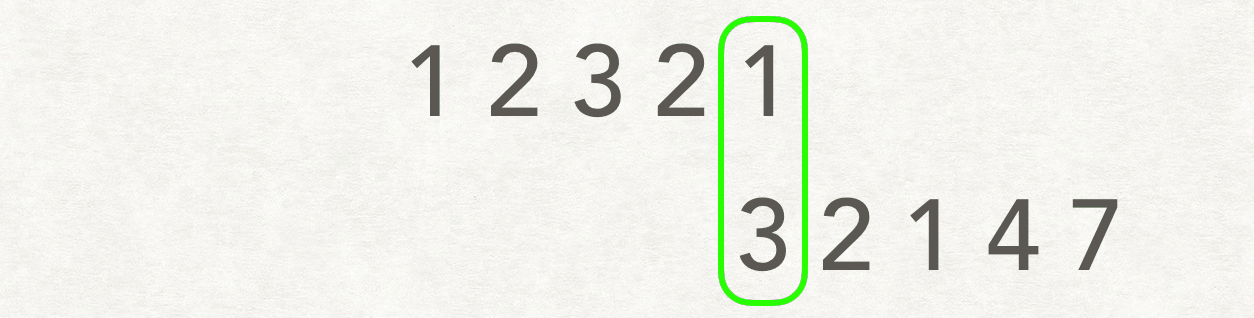
出处:小马的笔记
我觉的这个gif能很好的表示滑动窗口的做法
1.先固定A,移动 B,逐个寻找公共子数组中的长度
2.反之,固定B,移动A,寻找公共子数组中的长度
3.对比寻找处最大的公共子数组长度
for (int i = 0; i < lenA; ++i) {
int len = Math.min(lenB, lenA - i);
//先固定B的位置,即B数组的下标为0
int maxLen = finMaxLen(A, B, i, 0, len);
ans = Math.max(ans, maxLen);
}
/**
* Solution:: finMaxLen
* <p>寻找len长度内,两个数组的最长公共子数组/p>
* <p>HISTORY: 2020/7/1 liuha : Created.</p>
* @param A A数组
* @param B B数组
* @param addA A数组的滑动开始的下标,0下标表示当前数组为固定的数组
* @param addB B数组的滑动开始的下标,0下标表示当前数组为固定的数组
* @param len
* @return 最长公共子数组的长度长度
*/
private int finMaxLen(int[] A, int[] B, int addA, int addB, int len) {
int ret = 0, k = 0;
for (int i = 0; i < len; i++) {
if (A[addA + i] == B[addB + i]) {
k++;
} else {
k = 0;
}
ret = Math.max(ret, k);
}
return ret;
}
这个思路又借鉴官方的写法,我觉得官方的写法更优雅,这里将时间复杂度降到了O((N+M)×min(N,M)),
但我们遍历完A数组别忘记,还要固定A数组,遍历B数组
for (int i = 0; i < lenB; ++i) {
int len = Math.min(lenA, lenB - i);
int maxLen = finMaxLen(A, B, 0, i, len);
ans = Math.max(ans, maxLen);
}
DP
我们假设dp[i][j] 表示 A[] 和 B[]的最长公共前缀,i,j分别是数组的下标,那么答案即为所有 dp[i][j] 中的最大值。
我们以示例
A: [1,2,3,2,1]
B: [3,2,1,4,7]
如表格所示,我们需要的在坐标为 (0,2)(1,3)(2,4)
| |1|2|3|2|1|A数组
-------- | -----| -----| -----| -----| -----| -----
3| | |1 || |
2| | 1| |1 | |
1|1| | | | 1|
4|| | | | |
7|| | | | |
B数组|

存在的规律
1.下标存在dp[i][j]-->dp[i+1][j+1]->dp[i+2][j+2]
2.如图中箭头指向,当A[i]==B[j]时dp[i][j]=dp[i+1][j+1]+1,或者理解为A[i-1]==B[j-1]时dp[i][j]=dp[i-1][j-1]+1,
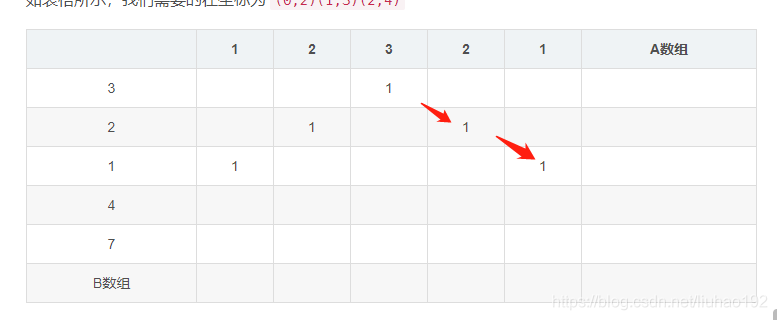
那就可以整理处DP的状态公式了
dp[i][j]=dp[i+1][j+1]+1 if(A[i]==B[j])
由于dp[i][j]从``dp[i+1][j+1]得到,所以我们要反过来遍历数组
for (int i = lenA - 1; i >= 0; i--) {
for (int j = lenB - 1; j >= 0; j--) {
dp[i][j]=A[i]==B[j]?dp[i+1][j+1]+1:0;
ans=max(ans, dp[i][j]);
}
}
或者使用另一个状态公式遍历
for (int i = 1; i <= lenA; i++) {
for (int j = 1; j <= lenB; j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
ans = max(ans, dp[i][j]);
}
}
}