每日题解:LeetCode 67. 二进制求和
2020-06-23
题目描述
给你两个二进制字符串,返回它们的和(用二进制表示)。
输入为 非空 字符串且只包含数字 1 和 0。
示例 1:
输入: a = "11", b = "1"
输出: "100"
示例 2:
输入: a = "1010", b = "1011"
输出: "10101"
提示:
每个字符串仅由字符 '0' 或 '1' 组成。
1 <= a.length, b.length <= 10^4
字符串如果不是 "0" ,就都不含前导零。
解法
JAVA
字符翻转
class Solution {
public String addBinary(String a, String b) {
int len = a.length() > b.length() ? a.length() : b.length();
int aLen = a.length();
int bLen = b.length();
int carry = 0;
StringBuffer ans = new StringBuffer();
//补充 0;
for (int i = 0; i < len; i++) {
int sum=carry;
sum+= (i <aLen) ? a.charAt(aLen-1-i) - '0' : 0;
sum+= (i <bLen) ? b.charAt(bLen-1-i) - '0' : 0;
int curr= sum%2;
carry=sum/2;
ans.append(curr);
}
ans.append(carry == 1 ? carry : "").reverse();
return ans.toString();
}
}
数组
class Solution {
public String addBinary(String a, String b) {
int len = Math.max(a.length(),b.length());
//将两个字符串转换为等长的
char[] s1 = new char[len];
char[] s2 = new char[len];
int aLen=a.length()-1;
int bLen=b.length()-1;
for (int i =len-1; i>=0; i--) {
if(aLen>=0){
s1[i]=a.charAt(aLen);
aLen--;
}else s1[i]='0';
if(bLen>=0){
s2[i]=b.charAt(bLen);
bLen--;
}else s2[i]='0';
}
char[] s3 = new char[len + 1];
int carry = 0;
for (int i =len-1; i>=0; i--) {
int sum=carry;
sum+= s1[i] - '0';
sum+= s2[i] - '0';
int curr= sum%2;
carry=sum/2;
//转换int 为char
s3[i+1]= (char) (curr+'0');
}
if (carry == 0) {
char[] temp = new char[len];
for (int k = 0; k < len; k++) {
temp[k] = s3[k + 1];
}
return new String(temp);
}
s3[0]='1';
return new String(s3);
}
}
解题思路
解法思路还模拟二进制加法做法,稍微注意的地方是二进制中是「逢二进一」。所以在最好的计算完成的时候需要判断是否还需要进位,比如11和1,由于第二步的运算需要进位,最后就变成了110
模拟
如下所示,模拟1010和1011相加的过程
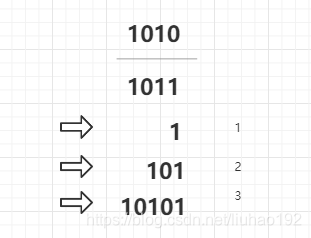
我们使用一个变量 carry 表示上一个位置的进位,初始值为 0。使用a,b代表当前需要进行运算的位置的值,每次运算都需要将carry +a+b,直到运算结束,然后判断carry是否需要进行进位的操作。
这里需要考虑到a,b两个字符串的长度不一致,在遍历过程中会出现短字符下标越界的问题。
for (int i = 0; i < len; i++) {
int sum=carry;
sum+= (i <aLen) ? a.charAt(aLen-1-i) - '0' : 0;
sum+= (i <bLen) ? b.charAt(bLen-1-i) - '0' : 0;
int curr= sum%2;
carry=sum/2;
ans.append(curr);
}
len表示a,b字符串最长的字符长度,这里我们需要判断当前遍历计数i是否取值字符的长度,大于了我们就取0,避免出现下标越界的问题,也可以考虑使用双变量进行计数,由于觉得可读性差就没这么写
//觉得这么遍历可读性很差
for (int i = charsA.length - 1, j = charsB.length - 1; i >= 0 || j >= 0; i--, j--)
{}
最后遍历结束后,需要判断最后一次运算是否需要进位,同时将字符翻转
ans.append(carry == 1 ? carry : "").reverse();
return ans.toString();
补零
字符的拼接的时候,由于是从左往右拼接的,答案是从右往左的,所以需要翻转字符串,能不能不翻转呢?
这里就可以还是延续模拟的思路,但是采用了补零,比如11和1运算,我们先做补零的操作,转换为
11和01运算
int len = Math.max(a.length(),b.length());
char[] s1 = new char[len];
char[] s2 = new char[len];
int aLen=a.length()-1;
int bLen=b.length()-1;
for (int i =len-1; i>=0; i--) {
//需要从高位开始进行赋值,数组赋值结束后,爱开始补零的操作
if(aLen>=0){
s1[i]=a.charAt(aLen);
aLen--;
}else s1[i]='0';
if(bLen>=0){
s2[i]=b.charAt(bLen);
bLen--;
}else s2[i]='0';
}
由于答案最多比最长数组多一位,直接新建一个len+1的数组,然后进行遍历进行相应位置运算,当然还是少不了进位变量carry
运算的部分,可以使用if判断字符的值,进行运算,但是存在四种情况(0,0;0,1;1,0;1,1),代码的看起来比较难受,所以,还是用转int的做法
char[] s3 = new char[len + 1];
int carry = 0;
for (int i =len-1; i>=0; i--) {
int sum=carry;
sum+= s1[i] - '0';
sum+= s2[i] - '0';
int curr= sum%2;
carry=sum/2;
//转换int 为char
s3[i+1]= (char) (curr+'0');
}
if (carry == 0) {
char[] temp = new char[len];
for (int k = 0; k < len; k++) {
temp[k] = s3[k + 1];
}
return new String(temp);
}
s3[0]='1';
return new String(s3);
关于字符串的运算还可以参考这题43. 字符串相乘
接下来,每天的题解可能不按照每日一题的顺序了,尽量要求自己每天完成中等题目的解题笔记。