每日题解:LeetCode 215. 数组中的第K个最大元素

发表于: 2020-06-30 更新于: 2024-10-01 浏览: 559

题目描述

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

解法

JAVA

class Solution {
    public int findKthLargest(int[] nums, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<Integer>(k);
    for (int num : nums) {
        if (heap.size() < k){
            heap.offer(num);
        } else {
            if (num > heap.peek()){
                heap.poll();
                heap.offer(num);
            }
        }
    }
    return heap.peek();
    }
}

CPP

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
         int left=0,len=nums.size(),right=len-1;
        int target=len-k;
        int ans;
        while ((ans = partition(nums, left, right)) != target ) {
            if(ans<target){
                left=ans+1;
            }else if(ans>target){
                right=ans-1;
            }
        }
        return nums[ans];
    
    }

     int partition(vector<int> &vector, int left, int right) {
        int temp=vector[left];
        int leftIndex=left;
        for (int i = left+1; i <= right; ++i) {
            if(vector[i]<temp){
                leftIndex++;
                swap(vector, leftIndex, i);
            }
        }
        swap(vector, leftIndex, left);
        return leftIndex;
    }
     void swap(vector<int> &vector, int left, int right) {
        int temp=vector[left];
        vector[left]=vector[right];
        vector[right]=temp;
    }
    
};

解题思路

优先队列

这里是直接调用JAVA的API实现最小堆的做法，PriorityQueue(优先队列）优先队列的作用是能保证每次取出的元素都是队列中权值最小，即默认栈顶是最小元素
将元素的排序交给PriorityQueue进行维护，由于需要找到第K个最大元素，就是从大到小进行排序数组，找到倒数第k个元素，只要维护一个只有k大小的最小堆就可以了

遍历数组，
当堆的元素个数小于k时，直接添加到堆中
当堆的元素个数大于k时，当遍历的元素大于堆顶元素时，堆顶元素弹出，然后添加当前遍历的数组

 for (int num : nums) {
        if (heap.size() < k){
            heap.offer(num);
        } else {
            if (num > heap.peek()){
                heap.poll();
                heap.offer(num);
            }
        }
    }

减治法

这部分代码参考了李哥的题解
假设nums[target]是目标答案下标值，通过某方法将下标范围存放[0,target-1]比nums[target]小的值，比nums[target]大的值放在[target+1,nums..size()]范围内，由于答案是第k大的元素，按照自然顺序进行排序的，应该是target=nums..size()-k,当我们按照target左小右大思路存放数组元素，nums[target]就是我们最终的答案

nums[0] 到 nums[target - 1] 中的所有元素都不大于 nums[target]；
nums[target + 1] 到 nums[,nums..size()]] 中的所有元素都不小于 nums[target]
我们以[3,2,1,5,6,4] 为例，第一次寻找比num[0]小的元素，下标停在元素1的位置

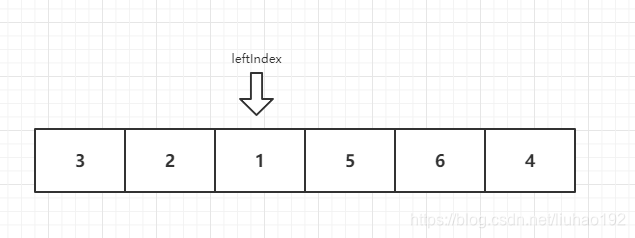
此时，leftIndex-1左边应该都是比num[0]小元素，leftIndex+1右边都是num[0]大的元素，这是我们还需要num[0]和leftIndex进行互换，

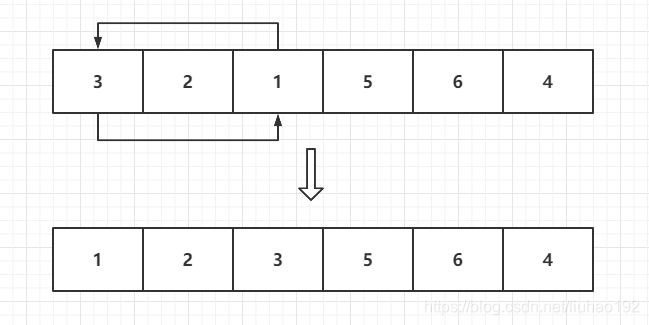
换个思路寻找第K个最大元素，其实就寻找第 target=nums.size()- k元素，我们只要保证target元素左小右大就可以了
这里我是将排序和赋值放到了whlie循环条件中，完成了排序和判断，当然也可以使用whlie(true)形成死循环阻塞，在while循环内进行赋值

int left = 0, len = nums.size(), right = len - 1;
        int target = len - k;
        int ans;
        while ((ans = partition(nums, left, right)) != target) {
            if (ans < target) {
                left = ans + 1;
            } else if (ans > target) {
                right = ans - 1;
            }
        }
        return nums[ans];

这里其实是快速排序的思路，每次我们选择一个数作为标记，待排序结束后，将标记存到其正确的位置

int partition(vector<int> &vector, int left, int right) {
        int temp = vector[left];
        int leftIndex = left;
        //遍历元素，发现当前元素比目前的元素小的就进行元素值互换，并且leftIndex下标往后移动，保存下一个比temp元素
        for (int i = left + 1; i <= right; ++i) {
            if (vector[i] < temp) {
                leftIndex++;
                swap(vector, leftIndex, i);
            }
        }
        //这里就是最后需要将当前值放到leftIndex位置上，这里其实就是图中所示的3和1的位置互换
        swap(vector, leftIndex, left);
        return leftIndex;
    }