每日题解:LeetCode 174. 地下城游戏
2020-07-12
题目描述
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
| -2 (K) | -3 | 3 |
|---|---|---|
| -5 | -10 | 1 |
| 10 | 30 | -5 ( P ) |
解法
java
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int n = dungeon.length, m = dungeon[0].length;
int[][] dp = new int[n + 1][m + 1];
for (int i = 0; i <= n; ++i) {
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
dp[n][m - 1] = dp[n - 1][m] = 1;
for (int i = n - 1; i >= 0; --i) {
for (int j = m - 1; j >= 0; --j) {
int minn = Math.min(dp[i + 1][j], dp[i][j + 1]);
dp[i][j] = Math.max(minn - dungeon[i][j], 1);
}
}
return dp[0][0];
}
}
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int [] dp = new int[n+1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[n-1] = 1;
for(int i = m-1; i >= 0; i--) {
for(int j = n-1; j >= 0; j--) {
dp[j] = Math.min(dp[j], dp[j+1]) - dungeon[i][j];
if(dp[j] <= 0) dp[j] = 1;
}
}
return dp[0];
}
}
解题思路
DP(动态规划)
从题目可以得到
- 骑士到达右下角的坐标时,最低的血量至少为1,但是题目要求是最低初始健康点数,那么只能为1
- 每个坐标的,只能是从其左边和上的方向进入
假设dp[i][j]表示从坐标(i,j)到终点所需的最小初始值,得到dp[i][j]与min(down, up)的值有关系,但是这种正向更新dp无法更新当前所需最小的生命值,所以就换个思路,放心更新,由dp[i+1][j],dp[i][j+1]的值更新当前dp[i][j]的值,这里,由于我们需要维护一个dp[i][j]的最小值,如果当前的dungeon[i][j]<0,那么Math.min(dp[j], dp[j+1])则需要加上|dp[i][j]|的绝对值,反而dungeoni][j]>0,那么Math.min(dp[j], dp[j+1])则需要减去|dp[i][j]|的值,同时我们还需要保证,初始值还必须大于等于 1,
以示例为例子
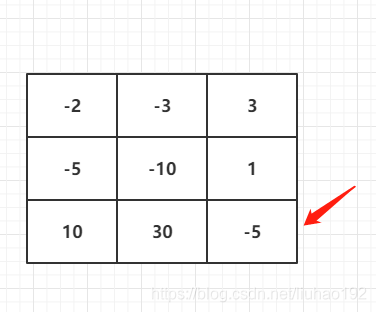
箭头指向的点的值为-5,由于只能进入1、30才能进入,骑士在1时,骑士在1的时候血量要为6;骑士在30时,虽然可以满足到-5点,但是无法满足骑士能够拯救到公主所需的最低初始健康点数,所以30的坐标的dp[j][i]=1(初始值还必须大于等于 1,),在1的坐标是为1-(-5)=6,
得到状态公式为
dp[i][j]=max(min(dp[i+1][j],dp[i][j+1])−dungeon(i,j),1)
实现代码
int minn = Math.min(dp[i + 1][j], dp[i][j + 1]);
dp[i][j] = Math.max(minn - dungeon[i][j], 1);
同时二维数组也可以进一步优化为一维数组不断原来的值,dp[j] = Math.max(1, Math.min(dp[j], dp[j + 1]) - dungeon[i][j]);