每日题解:LeetCode 1465. 切割后面积最大的蛋糕

题目描述

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离，类似地， verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出面积最大的那份蛋糕，并返回其面积。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7 取余后返回。

示例 1：

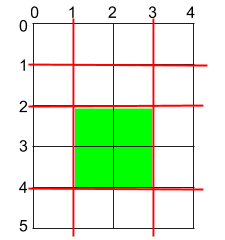
在这里插入图片描述

输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。
示例 2：
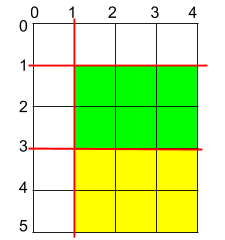
在这里插入图片描述

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6

解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。
示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

2 <= h, w <= 10^{9

1 <= horizontalCuts.length < min(h, 10}5)
1 <= verticalCuts.length < min(w, 10^5)
1 <= horizontalCuts[i] < h
1 <= verticalCuts[i] < w
题目数据保证 horizontalCuts 中的所有元素各不相同
题目数据保证 verticalCuts 中的所有元素各不相同

解法

JAVA

class Solution {
    public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
        Arrays.sort(horizontalCuts);
        Arrays.sort(verticalCuts);
        int mod = 1000000007;
        int hSize = horizontalCuts.length;
        int wSize = verticalCuts.length;
        long maxM = h - horizontalCuts[hSize - 1];
        long maxN = w - verticalCuts[wSize - 1];
        maxM = Math.max(maxM,horizontalCuts[0]);
        maxN = Math.max(maxN,verticalCuts[0]);
        for (int i = 1; i <hSize; i ++) {
            maxM = Math.max(maxM,horizontalCuts[i] - horizontalCuts[i-1] );
        }
        for (int i = 1; i <wSize; i ++) {
            maxN = Math.max(maxN,verticalCuts[i] - verticalCuts[i-1] );
        }
        return  (int)((maxM * maxN ) % mod);
    }
}

CPP

class Solution {
public:
    static int maxArea(int h, int w, vector<int> &horizontalCuts, vector<int> &verticalCuts) {
        //排序
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        int hSize = horizontalCuts.size();
        int wSize = verticalCuts.size();
        int maxH = max(horizontalCuts[0], h - horizontalCuts[hSize - 1]);
        int maxW = max(verticalCuts[0], w - verticalCuts[wSize - 1]);
        for (int i = 1; i < hSize; i++) {
            maxH = max(maxH, horizontalCuts[i] - horizontalCuts[i - 1]);
        }
        for (int i = 1; i < wSize; i++) {
            maxW = max(maxW, verticalCuts[i] - verticalCuts[i - 1]);
        }
        int model = 1000000007;
        return int64_t(maxH) * int64_t(maxW) % model;
    }

};

解题思路

题目要求找出面积最大的那份蛋糕，那怎么才能找到最大的那块呢？那就最长和宽最大的那块就好了，那就踏上寻找最大的长和宽的征途吧！！
假设横向切的数组为[1, 2,4]，纵向切的数组为[1,3]

横向观察

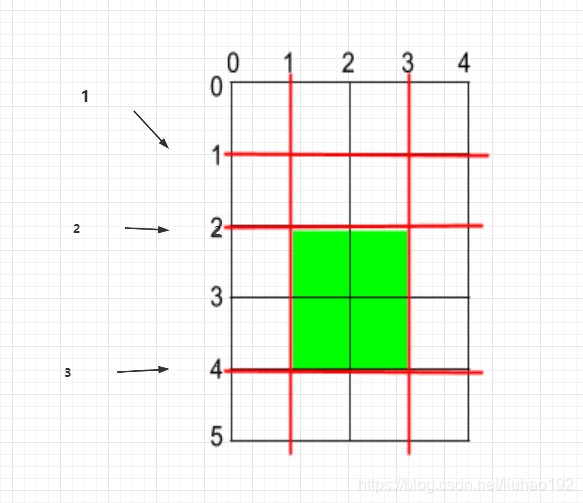
在这里插入图片描述
如图所示，1，2，3表示我们切入的顺序，最后的最大距离在2，4之间为2。
假设，我们换个思路，先从最大的那个数字开始切，

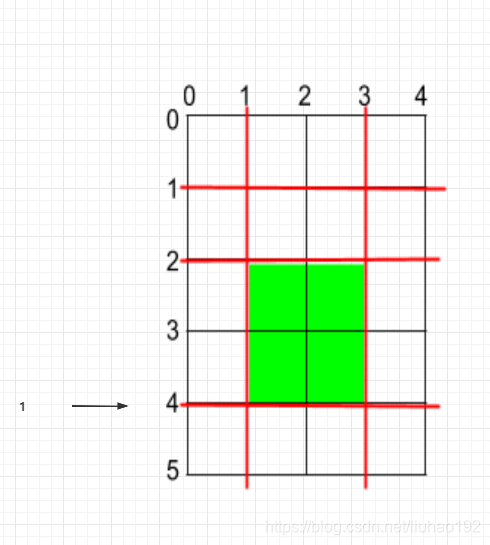
将横向的蛋糕切成0==>4， 4==>5两块，此时最大的那块是0==>4.长度为4；然后，我们换个方法从最小的数字开始切。
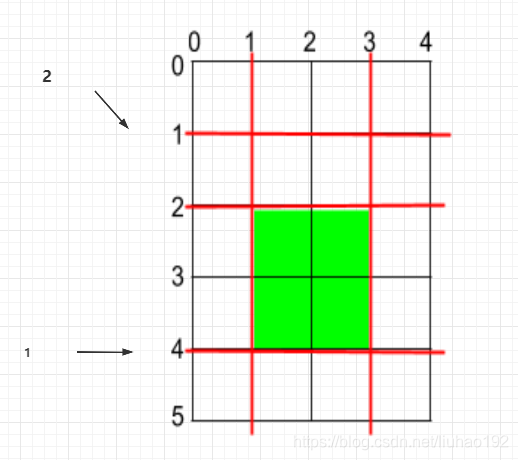
在这里插入图片描述
将横向的蛋糕切成0==>1， 1==>4，4==>5两块，此时最大的那块是1==>4.长度为2；然后我们切最后一刀

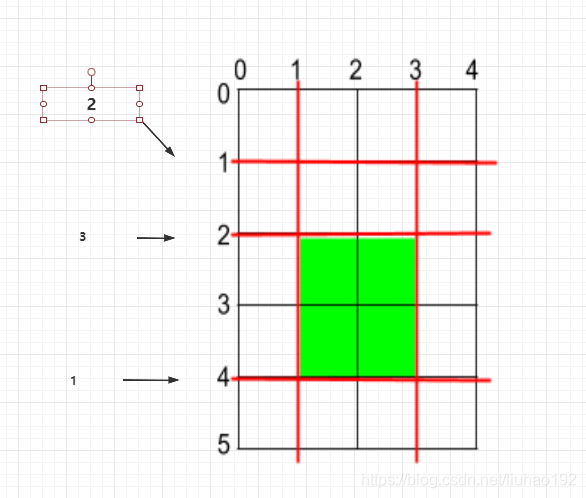
此时横向的蛋糕切成0==>1， 1==>2， 2==>4，4==>5两块，此时最大的那块是2==>4.长度为2；
当我们换了一个方式切蛋糕后，我们发现从第二刀开始，切的位置都在第一刀下去最大的那块上，即演示图中1==>4上。
那思路就这么归纳了，先排序要切的顺序，先切最大的那次,然后在遍历寻找最大距离。

int hSize = horizontalCuts.length;
long maxM = h - horizontalCuts[m-1];

这里设置为long是因为，最后根据题目由于答案可能是一个很大的数字,先设置为long,避免最后的乘积直接溢出。
如图，
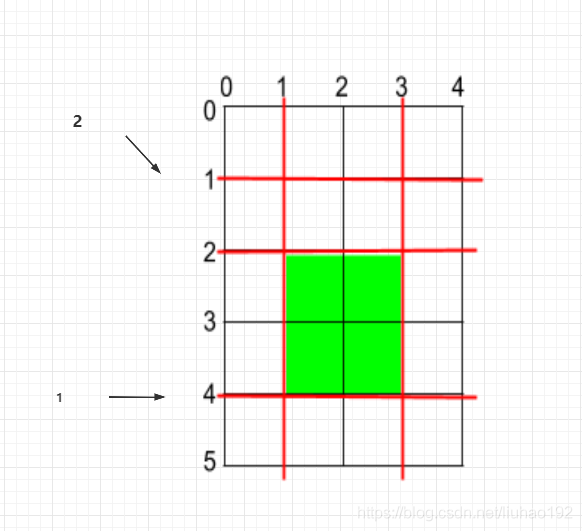
在这里插入图片描述
当我们切横向下第二刀的时候，此时最大的距离为4-1=3；两刀之前间距是两个元素的差。
这里我们优先将horizontalCuts[0]的距离先比较，因为我们数组遍历要从i和i-1进行比较，先比较避免出现数组越界，当然也可以扩容数组，在头设置一个为0的元素。

 maxM = Math.max(maxM,horizontalCuts[0]);

遍历数组，比较两刀之间距离，寻找最大的距离

//从1开始遍历
for (int i = 1; i <hSize; i ++) {
maxM = Math.max(maxM,horizontalCuts[i] - horizontalCuts[i-1] );
}

纵向

同理纵向的思路也一样

int wSize = verticalCuts.length;
//先切最大的那刀
long maxN = w - verticalCuts[wSize - 1];
 maxN = Math.max(maxN,verticalCuts[0]);
 for (int i = 1; i <wSize; i ++) {
  maxN = Math.max(maxN,verticalCuts[i] - verticalCuts[i-1] );
 }

还有一个原因，为什么比较数组末尾，避免最大的那块在第一刀的就已经出现，假设h=5，horizontalCuts={1，2}，切最大的那次的时候，最大已经出现了5-2=3;
扯点题外话吧，这题其实最近的一道周赛题目，当时，虽然，我已经有思路，需要最大的那块就可以了。
但是，我是按照数组的顺序去寻找的，在一个用例就出现了，一开始剩下的那块，大于了后面切的距离，当时，我一点思路都没，后来，看了大佬们的写法，才发现原来是可以排序的。还是题目遇到的少，作为平时都不接触算法的我，留下了后悔不学习的眼泪！！
这周，我想一篇关于List源码的文章，然后再分析Collection的类们是如何扩容的，偷偷告诉你，map虽然是Collection中的一员，它不是Collection的子类，周末再告诉你为什么，map被Collection抛弃了，map还对Collection依依不舍的故事。

清水1024