题解:LeetCode 14. 最长公共前缀

题目地址
个人博客地址

题目描述

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"
示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

解法

JAVA

public class Solution {
    public String longestCommonPrefix(String[] strs) {
        int len;
        if (strs == null | (len = strs.length) == 0) {
            return "";
        }
        String prefix=strs[0];
        //遍历数组
        for (int i = 1; i < len; i++) {
            prefix=getCommonPrefix(prefix,strs[i]);
            if(prefix.length()==0){
                return  "";
            }
        }
        return  prefix;
    }

    private String getCommonPrefix(String prefix, String str) {
        int length = Math.min(prefix.length(), str.length());
        for (int i = 0; i < length; i++) {
            if(prefix.charAt(i) != str.charAt(i)){
                return prefix.substring(0, i);
            }
        }
        return prefix.substring(0, length);
    }
}

CPP

class Solution {

public:
     string longestCommonPrefix(vector<string>& strs) {
        if (!strs.size()) {
            return "";
        }
        return  longestCommonPrefix(strs,0,strs.size()-1);
    }

     string commonPrefix(const string left, const string right) {
        int minLength  = min(left.size(), right.size());
        int index = 0;
        while ( index < minLength && left[index] == right[index] ) {
            index++;
        }
        return left.substr(0, index);
    }

       string longestCommonPrefix(const vector<string>& strs, const int start, const int end) {
        //中止条件
        if(start==end){
            return strs[start];
        }
       int mid=(start+end)>>1;
        string left=longestCommonPrefix(strs,start,mid);
        string right=longestCommonPrefix(strs,mid+1,end);
        return  commonPrefix(left,right);
    }

};

解题思路

遍历

如图所示，以["flower","flow","flight"]为例子，依次遍历字符串数组中的每个字符串，对比两个字符串，得出两个字符串的最长公共前缀，然后将当前的最长公共前缀和下一个字符串继续对比，遍历结束后就能得到公共的最长前缀。
如果在遍历过程，当前公共前缀的为""，就可以提前结束遍历，不要再遍历下去

if(prefix.length()==0){
 return  "";
}

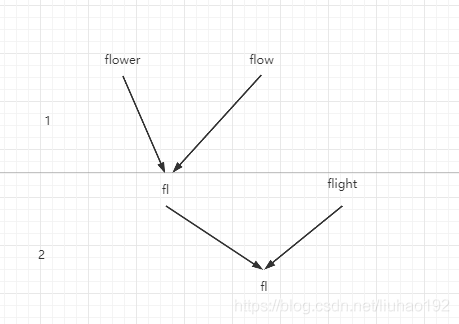
对比两个字符串时，由于最长公共前缀，两者都存在，我们只要在最短的字符串寻找便可以了，遍历对比的次数上限为最短的字符串

private String getCommonPrefix(String prefix, String str) {
        int length = Math.min(prefix.length(), str.length());
        for (int i = 0; i < length; i++) {
         //当字符不相等时，返回截取的字符
            if(prefix.charAt(i) != str.charAt(i)){
                return prefix.substring(0, i);
            }
        }
        return prefix.substring(0, length);
    }

分治法

我们逐个遍历的话，时间复杂度O(mn)，其中 m 是字符串数组中的字符串的平均长度，n 是字符串的数量。
既然最长公共前缀存在每个字符串中，我们能不能这样的思路进行查找呢？
在这里插入代码片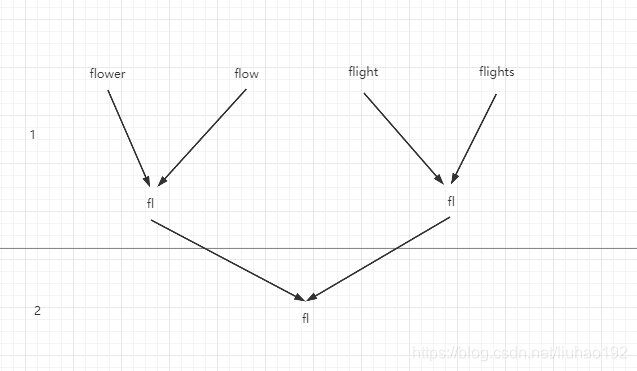
我们将数组分为左右两个部分，然后左右部分需要其的最长公共前缀，然后再将这左右部分的最长公共前缀再对比寻找答案的最长公共前缀。

    int mid=(start+end)>>1;
        string left=longestCommonPrefix(strs,start,mid);
        string right=longestCommonPrefix(strs,mid+1,end);
        return  commonPrefix(left,right);

将数组分为左右两个部分，然后开始寻找他们的最长公共前缀

    string commonPrefix(const string left, const string right) {
        int minLength  = min(left.size(), right.size());
        int index = 0;
        //循环对比字符，直到字符不相同时，截取字符
        while ( index < minLength && left[index] == right[index] ) {
            index++;
        }
        return left.substr(0, index);
    }

那什么时候结递，我们拆分到最后一个字符串，就停止递归

if(start==end){
return strs[start];
}

当然，使用分治的方法和遍历，本质上没有很大的差别，都是遍历整个数组，官方题解提到使用二分法的减少时间复杂度，可以参考一下。