每日题解:LeetCode 1028. 从先序遍历还原二叉树

题目地址

题目描述

我们从二叉树的根节点 root 开始进行深度优先搜索。

在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（如果节点的深度为 D，则其直接子节点的深度为 D + 1。根节点的深度为 0）。

如果节点只有一个子节点，那么保证该子节点为左子节点。

给出遍历输出 S，还原树并返回其根节点 root。

示例 1：
输入："1-2--3--4-5--6--7"
输出：[1,2,5,3,4,6,7]


示例 2：

输入："1-2--3---4-5--6---7"
输出：[1,2,5,3,null,6,null,4,null,7]


示例 3：
输入："1-401--349---90--88"
输出：[1,401,null,349,88,90]

提示：

原始树中的节点数介于 1 和 1000 之间。
每个节点的值介于 1 和 10 ^ 9 之间。

解法

JAVA 迭代

public class Solution {
    public TreeNode recoverFromPreorder(String S) {
        int len = S.length();
        //"1-2--3--4-5--6--7"
        Stack<TreeNode> stack = new Stack<>();
        int pos = 0;
        while (pos < len) {
            int level = 0;
            while (S.charAt(pos) == '-') {
                pos++;
                level++;
            }
            char value;
            int num = 0;
            while (pos<len && Character.isDigit(value = S.charAt(pos))) {
                num = num * 10 + (value - '0');
                pos++;
            }
            TreeNode node = new TreeNode(num);
                if (level == stack.size()) {
                    if (!stack.isEmpty()) {
                        stack.peek().left = node;
                    }
                }else {
                    while (level != stack.size()){
                        stack.pop();
                    }
                    stack.peek().right= node;
                }
            stack.push(node);
        }
        while (stack.size()>1){
            stack.pop();
        }
        return stack.peek();
    }
   }

CPP 递归

class Solution {
public:
    TreeNode *recoverFromPreorder(string s) {
        return dfs(0, s);
    }
    int pos = 0, level = 0;
    TreeNode *dfs(const int &depth, const string &s) {
        int num = 0;
        for (; pos < s.length() && s[pos]!= '-'; pos++) {
            num = num * 10 + s[pos] - '0';
        }
        level = 0;
        while (pos < s.length() && s[pos] == '-') {
            level++;
            pos++;
        }
        TreeNode *node = new TreeNode(num);
        if (level > depth)
            node->left = dfs(level, s);
        if (level > depth)
            node->right = dfs(level, s);
        return node;

    }

};

解题思路

分析题目可以得到

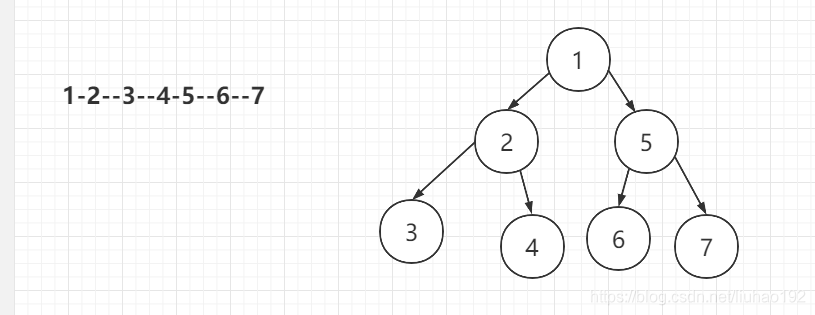
• 字符 - 的个数，表示树的深度：比如-2，-5就是深度为1，2是左子树，5是右子树
• 字符 -的后数字，表示节点的值

迭代

迭代的写法，首先我们先拆分字符得到深度和数字

int pos = 0;
.....
  int level = 0;
  //遍历 -字符
 while (S.charAt(pos) == '-') {
pos++;
level++;
}

由于我们读取的数字字符都是单个的，比如14，我们分别读取到1和4，所以需要*10，进行计算

char value;
int num = 0;
 while (pos<len && Character.isDigit(value = S.charAt(pos))) {
 num = num * 10 + (value - '0');
 pos++;
}

拆完字符 -和数后，我们遇到一个问题，怎么保存我们得到的值，并且可以继续保存往下遍历节点？
我们使用栈，利用栈的后入先出的特点，保存从根节点到当前节点的路径上的所有节点，同时也可以回溯到之前的节点，比如-5就需要回溯到1节点

Stack<TreeNode> stack = new Stack<>();
....遍历代码
stack.push(node);

由于先序遍历的特点，先遍历全部左子树，然后再从最后一个节点开始遍历右节点()

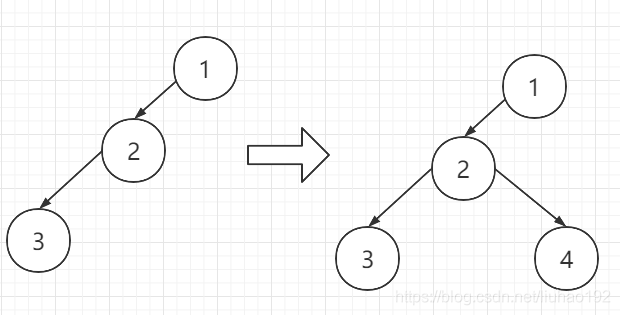
当我们遍历左子树时，每次遍历一个新节点时，此时的深度level和栈的size()相等，所以我们将节点存入栈，同时将栈顶元素的左子树指向我们当前的节点

 TreeNode node = new TreeNode(num);
if (level == stack.size()) {
if (!stack.isEmpty()) {
stack.peek().left = node;
}

当我们开始遍历右节点的时候，就会出现深度和栈的个数不一致的情况

while (level != stack.size()){
 stack.pop();
}
stack.peek().right= node;

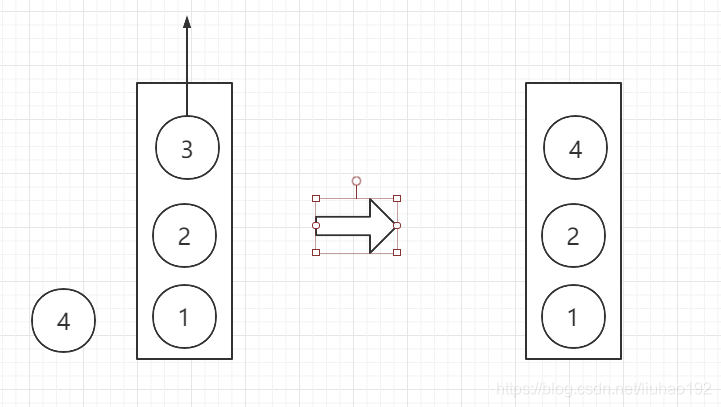
• 此时栈的个数为3，深度为2，我们要加入4这个的节点，但是4这个节点和3深度一样的，并且是2的右子树，所以，我们将3节点弹出，同时栈顶节点2的右子树指向当前节点4
• 同理下一个节点5，深度和栈的个数不一致，我们就继续弹出，直到level和栈的size()相等，然后把栈顶的右子树指向5节点

当我们遍历完字符时.此时栈的情况如下所示，我们需要1这个节点，所以就要把弹出不要的元素，直到栈只有根节点

while (stack.size()>1){
stack.pop();
        }
return stack.peek();

迭代的最关键思路在这块代码，

  TreeNode node = new TreeNode(num);
                if (level == stack.size()) {
                    if (!stack.isEmpty()) {
                        stack.peek().left = node;
                    }
                }else {
                    while (level != stack.size()){
                        stack.pop();
                    }
                    stack.peek().right= node;
                }
            stack.push(node);

递归

递归的写法，我们先搬出dfs的模板，

public Node dfs(...){

    //...逻辑
    root = ...
    //...逻辑
    root.left = ...
    //...逻辑
    root.right = ...
    //...逻辑
    return root;
}

读取字符的代码和迭代的写法差不多

//全局变量 pos遍历的字符位置
int pos = 0, level = 0;
.....
int num = 0;
//这里可以用whle写，java写法用例while
for (; pos < s.length() && s[pos]!= '-'; pos++) {
            num = num * 10 + s[pos] - '0';
}
level = 0;
 while (pos < s.length() && s[pos] == '-') {
level++;
 pos++;
}

然后套用模板的写法

TreeNode *node = new TreeNode(num);
 //...逻辑
node->left = dfs(level, s);
 //...逻辑
node->right = dfs(level, s);
 //...逻辑
return node;

然后在考虑中止条件，我们使用depth维护当前节点深度，如果level>depth时，表明其存在子节点，则需要继续往前遍历，当level=depth，则返回当前的节点，退回到上一个递归，继续除非其右子树的查找，由于当前的pos已经往后移动了，开始遍历其右节点

• 比如先遍历1节点，此时我们开始的深度为0，此时level为1，将下一个遍历的值作为其左节点，当遍历完3节点时，此时depth=2，level=2，返回当前节点，退回上一个递归，

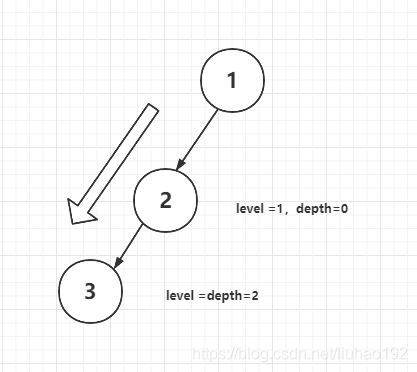
• 即2节点的右节点查找，

node->right = dfs(level, s);

此时pos指向了4节点，然后depth=1，level=1，返回当前节点，
由于之前2节点之前的depth=1，4读取到字符'-'就一个，，返回当前节点，

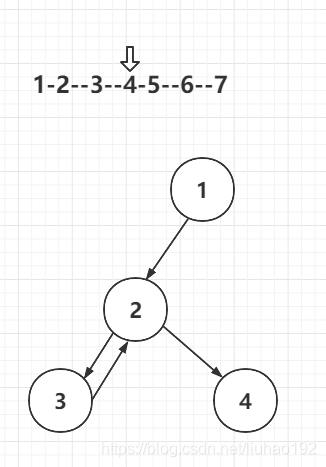
• 退回上一个递归，依次类推

所以整个递归代码为

static TreeNode *dfs(const int &depth, const string &s) {
        int num = 0;
        for (; pos < s.length() && s[pos]!= '-'; pos++) {
            num = num * 10 + s[pos] - '0';
        }
        level = 0;
        while (pos < s.length() && s[pos] == '-') {
            level++;
            pos++;
        }
        TreeNode *node = new TreeNode(num);
        if (level > depth)
            node->left = dfs(level, s);
        if (level > depth)
            node->right = dfs(level, s);
        return node;

    }